Les méthodes décrites dans la littérature sont quelquefois difficiles à comprendre et à appliquer précisément. Elles concernent plus particulièrement le marin, quelquefois le navigateur aérien, plus rarement le terrien.

Première constatation : si les premiers ont un horizon bien défini, référence de toutes les mesures de " hauteur " angulaire du soleil ou des étoiles, il n’en est rien du petit citadin et dans beaucoup d’endroits au relief tourmenté du terrien en général. En contrepartie, le sol est généralement plus stable que la mer ou les airs et surtout l’observateur conserve la même position aussi longtemps qu’il le souhaite alors que les navigateurs, par nature, voyagent entre deux mesures!

Nous nous attacherons donc à décrire des méthodes permettant de trouver la position d’un lieu terrestre essentiellement fondée sur les positions occupées par le soleil dans la journée. Ce type de mesure n’est intéressant que si les enfants ont bien observé, décrit et compris les différents mouvements apparents du soleil au cours de la journée et au fil de l’année ou au moins pendant quelques mois. Ce type de mesures vient alors conforter l’ensemble des apprentissages et leur donne un sens véritable par la possibilité de prévoir et d’agir de manière raisonnée. En revanche, la technique seule sans la conscience de ce que l’on fait ne présente qu’un intérêt très limité.

La mesure de la latitude et de la longitude du lieu fixe où se situe l’observateur utilise deux propriétés fondamentales liées à la connaissance des mouvements apparents du soleil :

1. La course du soleil entre la culmination et le coucher du soleil s’effectue de manière quasiment symétrique à ce qui s’est passé entre le lever du soleil et la culmination. Les enfants ont pu abondamment observer ce phénomène s’ils ont fait des relevés quotidiens à des périodes différentes, à l’aide d’un gnomon par exemple. Nous utiliserons cette symétrie pour déterminer l’heure du midi solaire vrai local bien plus précisément qu’en essayant " d’attendre " le moment où le soleil est au plus haut. Cette donnée, l’heure du midi solaire vrai local (notée HML dans la suite) est totalement liée à la longitude du lieu comme nous le verrons.
2. La forme de la trajectoire apparente du soleil au cours d’une journée donnée est représentative de la latitude du lieu, en particulier la hauteur angulaire qu’il occupe à la culmination, c’est à dire lorsqu’il passe sur le méridien céleste local. Si la première mesure nous permet de connaître l’heure du midi solaire vrai local, il nous suffira donc de déterminer le plus précisément possible cet angle, formé par la direction du soleil et la droite horizontale joignant le point de l’horizon au sud de l’observateur (en tout cas dans notre hémisphère).

Prenons un exemple simple pour commencer : le jour de l’équinoxe de printemps ou d’automne.

Nous avons vu (voir le document "Terre/Lune/Soleil" ) que ce jour-là la terre occupe une position très particulière dans sa révolution autour du soleil : l’axe terrestre est à l’instant de l’équinoxe parfaitement perpendiculaire à la direction Terre-Soleil

En simplifiant, pendant cette journée l’observateur d’un lieu quelconque verra le soleil à midi dans une position " typique " de sa latitude : il le verra au zénith (hauteur 90°) à l’équateur (O° de latitude), sur l’horizon (hauteur 0°) au pôle (90° de latitude) et comme le montre le schéma suivant :

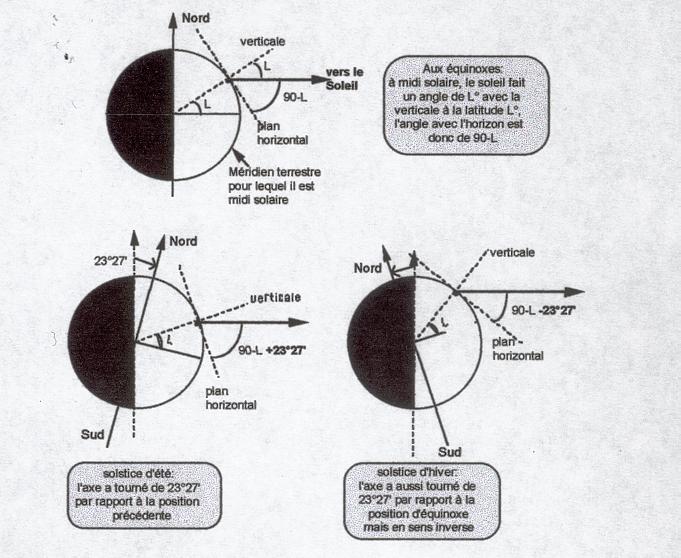
En tout point du globe, le soleil passe à midi solaire à une hauteur qui est le complémentaire de la latitude. C’est la relation inverse qui nous intéresse :

Si vous préférez utiliser l’angle formé entre la direction du soleil et la verticale du lieu, parfois plus facile à mesurer pour un terrien, dépourvu d’horizon bien défini mais disposant facilement d’une verticale de référence stable grâce à un fil à plomb, la relation est encore plus simple :

Cette relation très simple nous inciterait presque à ne faire cette mesure que le jour de l’équinoxe. Pourtant le reste de l’année n’est pas si complexe. En prenant cette position d’équinoxe en référence de ce que l’on appelle la déclinaison du soleil : angle formé entre l’équateur et la direction terre-soleil. Cet angle qui vaut 0° à l’équinoxe est aussi connu de nous aux solstices : 23°27’ Nord au solstice de juin et 23° 27’ Sud au solstice de décembre.

Ainsi, nous pourrions commencer à écrire une formule générale si nous convenons de noter la déclinaison négativement lorsque les valeurs sont dans l’hémisphère sud :

Hauteur angulaire du soleil à midi solaire vrai local = 90° - Latitude + Déclinaison.

Que nous abrègerons en :

HAmax = 90° - L + D

Et donc puisque ce qui nous intéresse est la latitude :

Ou, en utilisant cette fois l’angle avec la verticale à midi qui est donc minimal, Nmin

Cette relation ne semble pour l’instant fonctionner bien que 4 jours par an !

Si nous revenons sur le sens de la déclinaison qu’on peut aussi comprendre comme étant la latitude du point du globe qui reçoit le soleil au zénith (parfois appelé " Pied du Soleil " sur la Terre !), nous pouvons pourtant admettre qu’il s’agit bien d’une caractéristique de la trajectoire de la terre autour du soleil. Les valeurs de 0° reprise à chaque équinoxe, de +23°27’ au solstice de juin et de –23° 27’ au solstice de décembre ne sont que des cas particuliers d’un cycle qui se répète chaque année et dans lequel la terre occupe systématiquement les mêmes positions avec la même déclinaison tous les 365,2422 jours.

Si nous nous laissons aller à quelques simplifications " dangereuses " s’il s’agit de faire un point en mer, nous pourrions ainsi considérer que la table des déclinaisons se répète chaque année : à une date du calendrier correspond une déclinaison unique, un peu comme nous avons vu qu’à une date correspond pour un lieu donné (Paris dans le polycopié) une heure de lever et de coucher du soleil.

Quelles erreurs commettons-nous ?

• L’année durant 365,2422 jours, les mêmes jours de deux années successives ne correspondent pas rigoureusement aux mêmes points de la trajectoire, que l’année soit bissextile ou non !
• La déclinaison change à chaque instant alors que la fixer pour une journée quel que soit le lieu et donc l’heure du midi local revient à considérer qu’elle reste gentiment fixe en attendant de changer le lendemain!
• L’inclinaison de 23°27’ subit des variations au cours du temps liées au mouvement de nutation et plus généralement aux interactions complexes avec la lune et le soleil (entre autres !) au cours de la révolution.

En bref, la véritable table, que nous donnerons en fin de document pour l’année 2000 et qui indique les déclinaisons à 0 heures en T.U. (heure du méridien de Greenwich) et les variations de cette déclinaison au cours de la journée permettant ainsi aux marins de calculer précisément la déclinaison du soleil à midi au lieu où ils se trouvent, doit être recalculée chaque année. C’est l’une des missions du Bureau des Longitudes, en France.

Le calcul avec ces vraies données, précises au dixième de minute près, ne se justifie que lorsque les mesures effectuées sont issues d’instruments ayant la même précision que le sextant de marine. Les corrections instrumentales et de mesure sont alors nombreuses et complexes, loin de notre objectif. L’enjeu pour le marin est de taille : une minute de degré correspond à une erreur de position d’un mille nautique sur la carte. Nous allons allègrement commettre des erreurs de déclinaison et de mesure de plusieurs dizaines de minutes et donc de plusieurs dizaines de kilomètres sur la carte !

Commençons par la fin pour bien comprendre l’objectif : si nous savons à quelle heure légale en temps universel (UT) il est midi solaire vrai au lieu de notre mesure (HML) et si une table nous indique à quelle heure UT il est midi solaire vrai sur le méridien de Greenwich (HMG), quelquefois appelé " temps de passage " dans les tables, une simple soustraction entre ces deux données nous donnera le décalage horaire (DH) entre notre point et Greenwich. Si cette donnée est en heures en système décimal (par exemple 20 minutes = 0,3333 heures), il suffit de convertir ce décalage en temps en décalage en longitude (G) par rapport à Greenwich en multipliant ce temps par le nombre de degrés parcouru par la terre en une heure : 15 ° (soit 360°/24) en première approximation !

Un nombre négatif pour DH et donc pour G doit être traduit par une longitude Est (Le soleil passe au méridien du lieu avant de passer sur celui de Greenwich

La seule mesure que nous ayons à faire semble donc être de lire l’heure sur une montre réglée en TU lorsque le soleil passe au méridien. Plusieurs solutions :

Notons au passage qu’aucune de ces méthodes ne peut convenir à un navire faisant route puisque sa mobilité interdit aussi bien le plan stable de la troisième méthode que les deux points séparés de plusieurs heures de la deuxième. Le point doit donc être fait en partant d’un point estimé, fonction du dernier point, du cap suivi depuis et de la vitesse estimée du navire. On compare le point estimé qui, après calculs, conduit à une hauteur du soleil calculée, à la hauteur réellement mesurée à cet instant. Selon le sens et l’importance du décalage, on rectifie le point estimé d’un certain nombre de milles dans la direction du soleil ou dans la direction opposée (intercept). On voit donc l’importance énorme qu’il y a à faire le point très souvent et à reporter ce point sur la carte ainsi que les informations sur les caps suivis, les vitesses et les heures de changement de cap, les corrections ne pouvant avoir une chance de rapprocher de la position réelle que si les hauteurs estimées et les hauteurs mesurées ne sont que très peu différentes. Dans le cas contraire, seule la latitude peut être établie sûrement à la culmination mais il faudrait mettre le navire en panne pour tenter de retrouver la longitude !

Mais revenons sur le " plancher des vaches ". Quelle que soit la méthode, le but est d’obtenir la meilleure précision possible sur l’heure du midi. Là encore, toute erreur est immédiatement sanctionnée par une erreur conséquente de position sur la carte. En effet, une seconde d’arc d’écart correspond toujours à un mille nautique. Un degré de plus ou de moins sur les hauteurs relevées dans la deuxième méthode ou sur la position de la ligne nord-sud dans la troisième donne 4 minutes d’erreur (la Terre tourne de 360° toutes les 24 heures et donc de 1° toutes les 4 minutes, ou encore de 1 minute d’arc toutes les 4 secondes !).

Notre " petit degré " va donc décaler notre position sur la carte de… 240 milles nautiques ! Ajoutons-y les secondes de décalage entre notre montre et l’heure légale…

Voilà de quoi ramener nos prétentions à une très grande humilité. Le pointage des coordonnées mesurées sur la carte de France risque de ressembler à… un jeu de fléchettes… Mais ce n’est pas une raison pour ne pas le faire. Les enfants comprendront ainsi à la fois la méthode et la nécessité vitale pour un marin (dépourvu du système GPS, cela va de soi !) d’effectuer ces mesures avec la plus grande rigueur, en disposant d’instruments précis dont les erreurs systématiques sont connues et d’une bonne horloge conservant bien le temps de Greennwich. Le sextant et l’horloge de bord ne sont pas seulement des instruments chers, ce sont surtout des instruments précieux dont dépend la sécurité du navire, en cas de dysfonctionnement de l’électronique de bord.

Ces tables n’ayant pas été d’une simplicité enfantine à saisir et à construire, je ne recommencerai le travail pour les années suivantes que s’il est utile au moins à quelques instituteurs : qu’on se le dise !

Tirées des données fournies par le Bureau des Longitudes via le célèbre almanach du marin breton, elles donnent des valeurs d’une précision bien supérieure à ce qui nous est nécessaire, mais comme chacun le sait : qui peut le plus peut le moins ! J’ai donc conservé cette précision, je l’ai même améliorée au niveau des calculs de variations de déclinaison. Ainsi, nous ne pourrons pas accuser les tables d’être à l’origine de nos erreurs de " point ". De plus, quelqu’un disposant d’un instrument précis, sextant par exemple, pourra vérifier l’efficacité de son instrument… au bord de la mer et à condition d’appliquer les corrections d’usage!

Le report de ces données dans un tableur permet d’automatiser les calculs (voir fichier Excel joint si vous avez eu ce document sous forme informatique).

Voyons comment utiliser ce tableau sur l’exemple de la ligne de données du 1^er janvier.

La déclinaison Do est la déclinaison du soleil ce jour-là à 0h UT. Elle est de 23° 4,3’ Sud ce que j’ai traduit par

–23,0717° d’après les conventions adoptées plus haut. Notre mesure de hauteur du soleil à la culmination en vue de déterminer la latitude ne se faisant évidemment pas à cette heure, en tous cas en France, il nous faut corriger la déclinaison.

Si l’on souhaite être très précis, il suffit d’ajouter à Do le produit de la variation horaire v qui ce jour là vaut 0,00333° et du nombre d’heures en décimal écoulées depuis 0h UT : on regarde sa montre réglée en temps universel (heure légale française – 1h en hiver et –2h en horaire d’été) au moment de la culmination !

L’exemple du tableau pour 12h UT nous indique que –23,0717 + 0,00333 * 12 = -23,0317°. Si vous souhaitez éviter ce calcul, vous pourrez donc utiliser cette colonne qui ne devrait entraîner qu’une erreur bien minime sur la latitude ! Vous disposez maintenant de la déclinaison D au moment de la mesure

En appliquant la formule

avec la hauteur angulaire Hamax atteinte par soleil à midi ce jour là, vous obtenez ce que l’on aimerait être la latitude L du lieu. Supposons que nous ayons mesuré 18° ce 1^er janvier :

L = 90° - 18° – 23,0317° = 48,9683° N que nous arrondirons sans prétention à 49°.

La deuxième partie du tableau nous servira à déterminer la longitude G, une fois connue l’heure du midi local HML, heure médiane entre les instants repérés où le soleil occupe la même hauteur angulaire dans une même journée. Supposons que l’on ait ainsi obtenu le premier janvier : HML= 11 h 59mn 15s.

Le décalage horaire avec Greenwich est :

DH = 11h 59mn 15s – 12h 3mn 17s = - 4mn 2s = - 242s = - 242/3600 h = - 0,0672 h

G = - 0,0672 *15 = 1,008° E

A ce stade, la comparaison avec la carte nous inciterait certainement à laisser tomber cette dernière décimale !

Ce texte est accompagné d’un classeur Excel donnant des tables plus complètes concernant le soleil que celle donnée en fin de ce document, ainsi que des feuilles de calcul permettant :

• de calculer automatiquement les coordonnées d’un lieu en fonction des mesures décrites plus haut ;
• de calculer un éphéméride local en fonction des coordonnées d’un lieu géographique (y compris les heures de lever et de coucher du soleil, l’heure du midi solaire vrai local et la hauteur du soleil à midi
• de connaître toutes les positions (hauteur et azimut) du soleil pour un jour donné en un lieu quelconque.

La première feuille " intro " donne quelques renseignements de base aux utilisateurs. Nous allons nous attacher dans un premier temps à la compréhension de la deuxième feuille " données de base ".

Les seules colonnes qui doivent être saisies chaque année (même si les variations sont faibles d’une année à l’autre sont :

• la déclinaison du soleil Do à Oh UT pour chaque jour de l’année, c’est à dire la latitude du pied du soleil à 0hUT ;
• la longitude du soleil Ahvo à Oh UT pour chaque jour de l’année, c’est à dire la longitude du pied du soleil à 0h UT.

Les autres données sont calculées à partir de ces deux données de base pour chaque jour. Pour être extrêmement précis, il aurait fallu entrer aussi les valeurs exactes du " temps de passage " du soleil au méridien de Greenwich, qu’on trouve aussi dans les tables. Je l’avais fait dans un premier temps, mais cette colonne de données supplémentaires à saisir risquait de grever sérieusement la mise à jour du tableau année après année. Cette colonne est donc désormais calculée en fonction des deux données de base : qu’on se rassure, l’erreur commise ainsi est de l’ordre de la seconde et donc entraîne sur les relevés de position une erreur de l’ordre du ¼ de mille !

A chaque instant, la Terre qu’on peut considérer comme une sphère éclairée par le soleil, occupe une position dans l’espace qui dépend de ses deux mouvements fondamentaux de rotation autour de son axe à vitesse constante et de révolution autour du soleil selon les lois de Képler (voir poly " terre – lune – soleil). La position en question varie donc à chaque instant, ce qui n’empêche pas qu’à un instant donné, comme sur une photo, la sphère en question est illuminée par le soleil d’une manière totalement déterminée et unique : chaque point du globe " voit " (ou ne le voit pas si le point en question n’est pas dans l’hémisphère éclairé !) le soleil dans une situation totalement unique : la hauteur du soleil sur l’horizon ET son azimut (angle formé entre la direction du soleil abaissée sur l'horizon et le Nord) dépendent de la position du point d’observation et sont uniques à cet instant : la connaissance (mesure) de ces deux données simultanément, à un instant donné, nous permettraient d’ailleurs de déterminer entièrement les coordonnées géographiques du lieu où nous sommes.

Restons sur cet instantané : parmi tous les points du globe éclairés par le soleil, l’un d’eux va nous intéresser particulièrement : celui qui " voit " le soleil au zénith à cet instant, c’est à dire celui qui voit le soleil dans la direction de sa verticale vers le haut ou encore à une hauteur de 90° sur l’horizon : ce point unique est celui que l’on appelle " Pied du soleil " dans les manuels de navigation.

Dès que l’on s’éloigne de ce point, la hauteur du soleil sur l’horizon diminue de 90° jusqu’à atteindre 0° sur le cercle d’illumination (cercle séparant la zone de jour et de nuit à cet instant). Une hauteur donnée correspond donc à un cercle centré sur ce point : à un instant donné, la hauteur du soleil en un lieu ne dépend que de la distance au pied du soleil. Si nous ajoutons la deuxième donnée qu’est l’azimut du soleil, nous déterminons bien de manière unique un point sur ce cercle et donc les coordonnées du lieu d’observation, le calcul n’étant qu’un problème de géométrie sphérique que nous éviterons d'aborder... même dans ce complément ! A l’inverse, si nous connaissons les coordonnées du pied du soleil à chaque instant et les coordonnées du lieu d’observation, nous pouvons totalement prévoir la hauteur et l’azimut du soleil à chaque instant et de ce fait connaître les heures de chaque journée pour lesquelles la hauteur sera 0° (lever et coucher du soleil en ce lieu) ainsi que celle pour laquelle la hauteur sera maximale (midi solaire vrai local), on voit donc comment un éphéméride local peut-être entièrement déterminé pour tout lieu du globe !

Commençons par nous demander ce que fait le pied du soleil au cours du temps. Ce point subit les effets des deux mouvements fondamentaux : rotation et révolution.

Commençons par le plus rapide : la rotation. En ne considérant que ce mouvement, le pied du soleil se déplacerait sur un parallèle à une vitesse constante de 360° en une rotation complète (soit en 23h 56mn 4,9s !) et donc d’un peu moins de 15° par heure, sa latitude ne changerait pas et sa longitude (Ahvt) changerait linéairement en fonction du temps.

Si, maintenant, nous considérons uniquement le mouvement plus lent de révolution, la latitude du pied du soleil (Déclinaison D) évoluerait à cause des positions occupées par la Terre sur sa trajectoire, la direction de l’axe restant fixe : rappelons que cette latitude vaut 0° aux deux instants d’équinoxes, 23°27’ Nord au solstice de juin et 23°27’ Sud (-23°27’ dans nos tables) au solstice de décembre), la valeur de la déclinaison à d’autres instants dépend donc uniquement de la position du globe sur la trajectoire de révolution. En réalité, le mouvement de révolution qui ne s’effectue pas à vitesse constante, modifie aussi la longitude du soleil à chaque instant (si la terre ne tournait pas sur elle-même, le pied du soleil ferait un tour de la terre en un an, à une vitesse qui dépend de la vitesse de la terre sur sa trajectoire.

C’est donc la composition des deux mouvements de rotation et de révolution qui fait changer la longitude du soleil de 15° par heure en moyenne sur l’année, la vraie valeur instantanée dépendant de la position de la terre sur sa trajectoire ! (voir polycopié pour comprendre les conséquences sur " l’équation du temps ")

Les tables, pour être parfaitement exactes, devraient donc nous donner la position du pied du soleil… à chaque instant ! Ce qui est évidemment impossible puisque cela correspondrait à une infinité de valeurs. Nous nous contenterons donc des coordonnées exactes du pied du soleil à 0h UT pour chaque jour données par les éphémérides. Les valeurs à d’autres instants d’un jour donné seront calculées par interpolation entre les valeurs du jour à 0h UT (Do et Ahvo) et les valeurs du lendemain à 0h UT en considérant que la déclinaison D évolue linéairement en fonction du temps à partir de Do à 0h UT de d par heure

et que la longitude du soleil Ahv évolue linéairement, à partir de Ahvo à 0hUT, de a par heure

A une heure h donnée en temps universel, les valeurs estimées ainsi sont donc :

Pour ceux qui s’inquiéteraient de cette " approximation ", sachez que l’erreur commise ainsi à chaque instant est infime (très inférieure à une minute d’arc) ! Si c’était la seule cause d’erreur, elle serait du même ordre que celle commise avec le système GPS civil. Nous n’avons donc " que " 365 ou 366 doublets de données à saisir chaque année…

Si vous n’avez pas encore le revolver pressé sur la tempe, voici les formules utilisées pour connaître la hauteur H et l’azimut Z du soleil, à un instant donné, en fonction des coordonnées du soleil D et AHv et des coordonnées du lieu d’observation L et G, sans démonstration : c’est de la géométrie sphérique, secouez donc votre prof de maths préféré ou un bon manuel si vous le souhaitez !

CQFD et arrêtez de jouer avec la détente !

J.M. FRAS 1999/2000